国家自然科学基金委员会重大研究计划重点支持项目

高性能科学计算的基础算法与可计算建模——

相场数学模型及相关数学问题高精度数值方法

项目成果科普性介绍

 一、准晶的建模与计算    

材料是人类生活和生产的物质基础。从科技发展的历史来看，重大的技术革新往往起源于材料的革新，新技术的发展反过来又促进了新材料的研制。而今，人类已经跨入人工合成材料的新时代，金属材料、精密陶瓷材料、复合材料、纳米材料、软物质材料等得到迅速的发展，为现代社会发展奠定了重要的物质基础。人类发展各种新材料的目的是为了获得所需的功能。而材料功能是通过构成材料的基本单元，形成结构，由结构体现功能。因此对材料的研究，需要深入地理解材料的结构。结构一般可以分为有序和无序。在无边界限制下，有序结构可以分为周期(晶体)结构、准周期结构等。准周期结构又可以分为准晶结构、非共度调制结构等。

准晶结构是科学研究的热点和重点。简单来说，准晶结构具有旋转不变形，缺乏平移不变性，即不具有周期性。同时，数学上有非常多的分支领域来研究准晶结构，一个著名的例子是剑桥大学Penrose教授在二十世纪70年代初提出的Penrose拼砌(参见图1)。

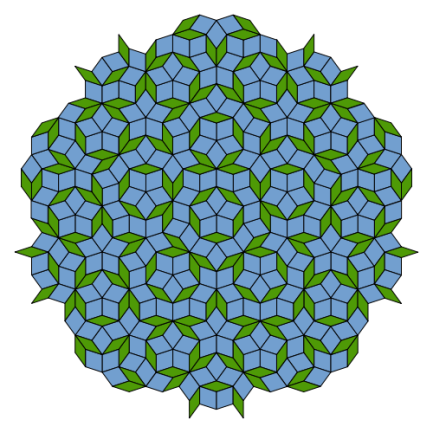
图1.Penrose拼砌.

从结构分类上看，准晶结构是一种介于晶体结构和无序结构之间的全空间有序结构。准晶结构最早由Shechtman于1982年在Al-Mn合金中发现(参见图2)。

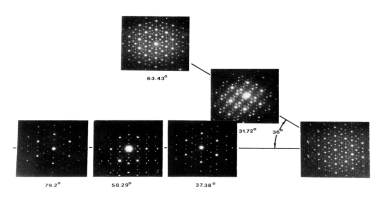
图2. D. Shechtman等人第一次在Al-Mn合金中发现准晶结构.

 迄今为止，人们已经在上百种金属合金，一系列的软物质体系，以及自然界中发现了大量的准晶结构。由于准晶结构具有不同于传统晶体的性质，比如准周期性，非晶体学对称性等，它的出现不仅改变了人们对物质结构的认识，也推动了现代晶体学、材料科学的革命。同时，准晶结构所具有的独特物理性质，比如高硬度、抗腐蚀性强、电子输运性质、低的热传导性、光子性质、原子迁移能力，使其拥有广泛的工业应用前景，推动了新型材料的开发。例如2018年Physics World评出的十大物理进展中就有超导准晶(参见图3)。超导现象是指固体的电阻在临界温度下会降低至零的现象。目前利用这种性质，超导材料已经科研和工业上已经得到了应用。超导准晶的发现也预测了另一种形式的超导性，这是基于准晶合金的几何结构来预测的。由于在准晶结构方面的工作，Shechtman获得了2011年诺贝尔化学奖。

图3. 超导准晶

通过理论或者数值计算预测材料的结构和性能是研究材料的重要手段之一。对于准晶材料而言，目前主要的计算方法是用一个非常大的周期结构来逼近准晶结构，这样就不可避免丟番图逼近误差，即在数论里面用有理数逼近无理数所出现的误差。因此在计算准晶材料及预测其性能上就会出现误差，尤其是需要高精度计算中。在我们的工作中，我们提出了一个计算准晶结构高精度的新型算法，即投影算法。这套算法可以推广到一般准周期系统的计算。我们已经将投影算法运用到非公度多尺度相场晶体模型的计算，得到了二维的12转、10转、8转旋转对称性的准晶结构，以及三维的二十面体准晶结构，预测了10转准晶结构的热力学稳定性。二维准晶结构的形态和相图参见图4。

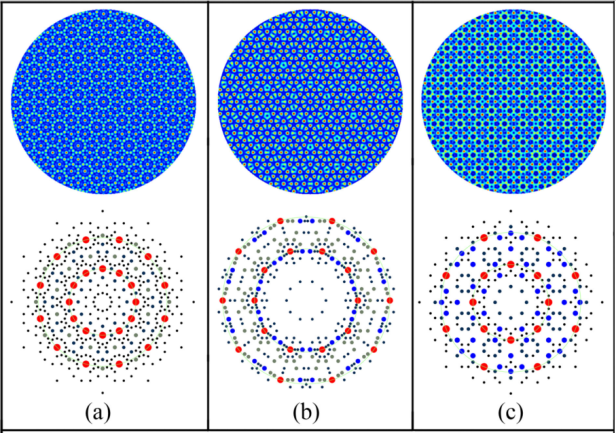
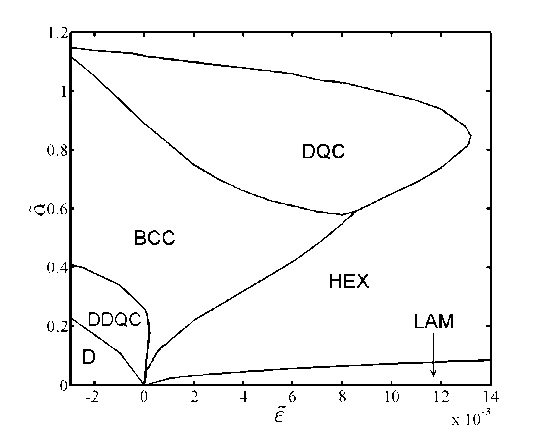
图4. 二维12转、10转、8转旋转对称性的准晶结构和相图

二、高维高阶问题有限元方法

有限元方法是在求解弹性力学问题中发明的，主要用于工程中弹性结构的应力分析。基于位移法的有限元应力分析是间接方法；基于Hellinger-Reissner变分原理的应力分析将应力和位移都作为独立变量直接离散，可以更好得满足平衡方程和应力边界条件，避免闭锁现象，而且可以得到更加精确的近似应力，是直接方法。从20世纪60年代开始，包括D.N.Arnold、Jim Douglas、Jr和混合有限元方法理论的奠基者F.Brezzi在内的很多国际著名数学家，一直在从事基于Hellinger-Reissner变分原理的弹性力学问题混合有限元的研究，做过很多尝试，并提出了应力弱对称的混合有限元方法；D.N.Arnold课题组基于数学上的弹性复形，首次得到应力严格对称的稳定混合有限元。这些进展的部分结果分别是F.Brezzi在1986年世界数学家大会的四十五分钟邀请报告和D.N.Arnold在2002年世界数学家大会的一小时邀请报告的主要内容之一。但其中的核心问题，即寻找应力严格（强）对称、有最优收敛性的稳定混合元，一直未得到有效解决。课题组的胡俊教授通过发现对称矩阵值H(div)元空间一个内蕴结构、获得两个基本代数结果、提出一个两步法的稳定性分析方法，构造出了以多项式为形函数、应力对称、有最优收敛阶的稳定混合有限元方法，设计了其自适应与快速算法，并建立了相应的数学理论，成功解决了该问题。

三、大规模离散代数系统的迭代法

课题组胡俊教授研究了线弹性力学问题混合有限元方法的快速迭代法，设计了一个分块对角预条件子和一个近似块分解预条件子，并分别用MINRES方法和GMRES方法求解预条件后的离散系统。这两个预条件子的设计和分析利用了鞍点系统在网格相关范数下一个新的稳定性结果。在该网格相关的范数下，应力的范数谱等价于L2范数，相应的矩阵是质量矩阵，容易求逆，位移的离散H1范数对应的矩阵谱等价于Schur补。我们设计了该Schur补其基于弹性力学方程组H1协调元的快速辅助空间预条件子的快速算法。对于对角和下三角的预条件子，我们证明了预条件后系统的条件数和网格参数及Lame常数都无关。

课题组杜魁教授针对大规模离散代数系统，直接对微分方程进行数值离散所得的线性系统的条件数通常都随离散点的个数增大而快速增大，导致非常病态条件的线性系统，因而很难精确和快速的求解。 利用微分方程的等价积分表达形式，可把微分问题转化为单位算子的紧扰动问题，利用谱方法对所得问题进行离散可得到好条件线性系统。利用此思想，可大大提高原问题的计算效率和精度。利用GMRES方法中出现的上Hessenberg矩阵的QR分解，找到了其R因子与GMRES残差向量范数之间的联系。利用矩阵特征值与特征多项式之间的联系，构造出了对应任意收敛曲线和容许调和Ritz值集的线性系统。利用两个Hessenberg -上三角矩阵束特征值反问题仔细分析了GMRES收敛性与Ritz值和调和Ritz值的关系。

四、表面活性剂的计算模拟

表面活性剂在精细化工领域、造纸工业、医药行业、化妆品行业、石油开采行业等等有重要的应用。表面活性剂的分子是由厌水的头部和亲水的尾巴组成，所以它们通常于停留在二相流的交界面上。表面活性剂能减小表面张力。表面活性剂的不均匀分布导致沿界面切线方向的Marangoni力，对宏观的流体动力学产生重要影响。有表面活性剂的二相流是一个高度非线性、多尺度、几何复杂的系统，它的计算模拟具有相当的挑战性。

 课题组徐建军副研究员对Reynolds传输定理做了修正，导出了表面活性剂质量的守恒律，提出了求解运动变形区域上对流扩散方程的基于水平集的扩散区域方法。徐建军副研究员将这些工作与之求解二相流的Navier-Stokes方程的投影方法、运动变形界面上对流扩散方程的欧氏水平集方法有效结合，提出了计算有可溶解表面活性剂的二相流的水平集方法，并通过大量二维、三维数值模拟实验，研究了可溶解表面活性剂对液滴运动的影响。这项研究工作对计算模拟表面活性剂的应用具有重要意义，产生了良好国际学术反响，多次收到国际学术会议报告邀请。

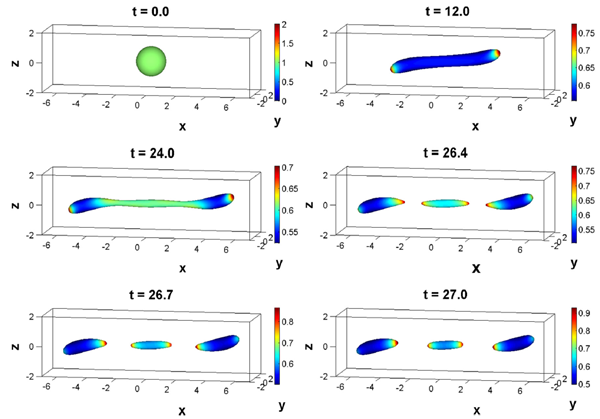
图1 剪切流作用下表面活性剂覆盖的液滴的分裂过程的模拟（颜色表示表面活性剂浓度）

 五、电磁波隐身材料建模与数值模拟

利用物体外形的离散信息得到了任意形状物体电磁波隐身的完美参数，证明了二维电磁隐身材料单轴色散的磁性材料，建立了电磁隐身问题的时域数学模型与数值方法。

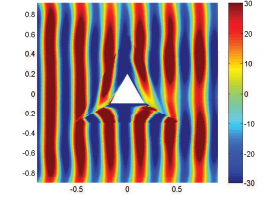
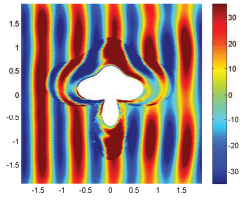
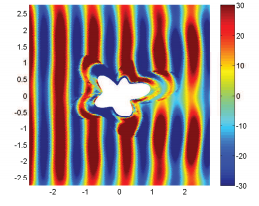
各种形状物体的电磁隐身的时域模拟。

六、有限元软件开发

团队基于Python语言开发了开源有限元软件包FEALPy。FEALPy 在 Github上的主页为 https://github.com/weihuayi/fealpy。FEALPy目前已经实现了各种类型的网格数据结构(包括多边形和多面体网格)、网格生成与优化、任意次的 Lagaragian 有限元空间(代码实现与空间维数无关)、任意次的二维虚单元空间、离散代数矩阵组装求解及可视化等丰富的基础功能模块。FEALPy 封装了各种常见的网格数据结构与算法细节，并提供统一网格数据接口，对应偏微分方程数值解理论及应用的研究者来说， 实现自己的数值实验程序，只需要考虑离散格式就可以了，不必纠结于网格的各种细节， 可大大提高相关研究者编写数值实验程序的效率。

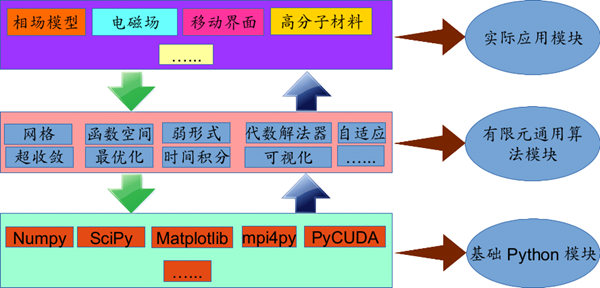
FEALPy软件框架示意图